

Next: Question:
Up: Theoretical identification of parameter
Previous: Motivation:
In DEB book Chap 3, {95}, we will see that the (volumetric)
structural length of an isomorph at constant food density X develops
during the juvenile and adult stage as
where the von Bertalanffy growth rate 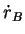 is given by
is given by
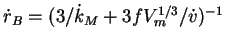 ,
and the
maximum length Vm1/3 by
,
and the
maximum length Vm1/3 by
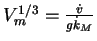 ,
and scaled functional response f is given by
,
and scaled functional response f is given by
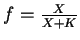 ,
where X is the food density and K the saturation
coefficient. Time t and food density X are variables (although Xis kept constant), and saturation coefficient K, energy conductance
,
where X is the food density and K the saturation
coefficient. Time t and food density X are variables (although Xis kept constant), and saturation coefficient K, energy conductance
 ,
maintenance rate coefficient
,
maintenance rate coefficient 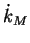 ,
investment ratio
g, (volumetric) length at birth Vb1/3 are parameters.
,
investment ratio
g, (volumetric) length at birth Vb1/3 are parameters.
Bas Kooijman
2000-12-14