

Next: Bibliography
Up: exam
Previous: Key words
The composition of liquid growth media is frequently given in its
ion composition in literature. The preparation of such media
from salts diluted in aqua dest leads to the practical problem of
how to combine available salts in a way best approximating the
given composition. Let us call the sought grams of salt
and the known molars of ion
. Elementary chemistry allows
us to compose a matrix , such that a typical element
stands for the molar contribution of 1 gram of salt 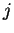 to ion
to ion  . If we want to prepare a litre of medium, the problem
is thus to find a useful , given and .
We can only hope for a unique solution if . Let us assume
this to be the case.
Let us first try to minimize the sum of the absolute errors. So,
we are looking for , such that
. If we want to prepare a litre of medium, the problem
is thus to find a useful , given and .
We can only hope for a unique solution if . Let us assume
this to be the case.
Let us first try to minimize the sum of the absolute errors. So,
we are looking for , such that
is minimal for all possible choices for . In matrix
notation we have
is minimal. To find such a , we have to solve
. In elements we have
In matrix notation this becomes
In terms of the latter notation, the solution is easily written down,
if it exists:
So, we have to multiply the column vector to the left
by the matrix
. This matrix is
known as the (left) generalized Moore inverse of the matrix .
It is an inverse, because multiplication by its original results in
the identity matrix,
. It
is generalized because originally, the inverse matrix is only defined
for square matrices. It is a particular generalized inverse, because
more ways exist to define an inverse matrix, namely the right
generalized inverse. The left and the right inverse are identical for
a symmetrical (and thus square) matrix only, if they exist.
Usually, the ions differ widely in abundance. From a
biological point of view, the way they play a role in supporting
life can be widely different. Therefore it is questionable wether
the loss function makes sense on physical grounds. A lot more
elegant is to minimize the sum of relative errors rather than the
absolute ones. The loss function now takes the form
In matrix notation we have
where
. In
elements, we have to solve
The solution, if it exists, is of course
Although this choice for will be satisfying in most
practical cases, it is possible that one or more elements of
are negative. Since it is far from easy to take a
certain salt out of a solution, we might want to have non-
negative solutions only. This has to be obtained by changing the
salts to be use for the preparation of the medium.
As an example, consider the preparation of artificial seawater,
as far as the main ions are concerned, from a set of salts. Table
8.1 gives the relevant data. An "exact" solution is not
possible, because the given combination of ions is not
electrically neutral. The values has been axtracted from "the
handbook", ignoring the many rare ions. We can conclude that,
when both magnesiumchloride and magnesiumsulfate are available,
the sum of relative errors can be made quite small. The option
with magnesiumsulfate only, has to be preferred above that with
magnesiumchloride only. In practice we should bother about how to
prevent gyps to precipitate, in this case.
Table 8.1:
The preparation of artificial seawater. The  -th element of the
matrix is obtained by dividing the
-th element of the
matrix is obtained by dividing the  -th element of the
main table given below, by the molar concentration of ion
-th element of the
main table given below, by the molar concentration of ion  of seawater
(second column) and the molar weight of salt
of seawater
(second column) and the molar weight of salt 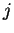 (second row). The last
three rows consist of the best choice for salts using one or both magnesium
salts in g/l. The first component indicates the sum of relative errors.
(second row). The last
three rows consist of the best choice for salts using one or both magnesium
salts in g/l. The first component indicates the sum of relative errors.
|


Next: Bibliography
Up: exam
Previous: Key words
Theoretische Biologie
2002-05-01