Stochastic self-ionization of water in cells

When a water molecule dissociates, one of its dipolar H-O bondsbreaks into a positively charged hydrogen ion, H, and a negatively charged hydroxyl ion, OH. The hydrogen ion, a proton,has a short lifetime as a free particle; its combines with a water molecule to form a hydronium ion, HO. This binding increases the valence angle of the water molecule from to , so making the added proton indistinguishable from the other two. The extra proton possibly jumps from one water molecule to another. The precise structure of liquid water is still not known with certainty, but for practical purposes it is still convenient to refer to the concentration of hydrogen ions in a solution, [H], even though what is really meant is the concentration of hydronium ions. The dissociation of water and the sociation of H and OH are, in the mean in an otherwise constant environment, equally fast processes and at C, we have . In a pure water, , which is frequently given in its log-transformed form: , where is expressed as mole per litre. The pH it one of the most important properties of a biological fluid. It influences e.g. enzyme activities; a change in pH can trigger cell growth and division; the movements of protons across a membrane, down the electrochemical gradient, is coupled to the synthesis of ATP in chloroplasts, mitochondria and bacteria. The pH is found to be regulated within a narrow band around a pH of 7, rather independent of the pH in the environment. Yet, there might be a lower limit to the fluctuations due to the stochastic behaviour of the dissociation of water. Think, for the sake of argument, of a bacterium of volume , consisting of pure water at C. For a specific density of , it weights g. The number of water molecules is some , while the number of protons is . The relatively small number of protons calls for a consideration of the stochastic fluctuation of the number of 'free' protons. We assume that each water molecule dissociates independently from the others with a constant probability rate of . The probability rate of the binding of a proton with a hydroxyl ion, is taken to be proportional to the product of their concentrations (and so with their numbers in a fixed volume) with a proportionality constant of . The number of protons, say , is necessarily the same as the number of hydroxyl ions because of electroneutrality and mass balance. We can safely neglect the decrease of the number of water molecules, say 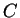$C$, due to dissociation. 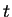If denotes the probability that the number of protons at time $t$ equals , we have for

where refers to the probability that more than one event (i.e. dissociation or binding) occurs during a time increment . If we bring the term to the left, divide by and let approach to zero, we arrive at

where denotes the derivative of with respect to the time. For we have

(11.3)

and so

(11.4)

which is a special case of (11.2) when we make the appointment that . So, (11.2) represents the stochastic model for the number of 'free' protons. By comparison, the corresponding deterministic model would be

(11.5)

Separation of variables and integration gives

(11.6)

where denotes the equilibrium number of 'free' protons in the deterministic model, which is given by , and the relaxation time, which is given by . At C, and (in ice, is faster!).This gives a relaxation time of some s. We now continue with a further analysis of the stochastic model. As long as we are interested in processes with relaxation times much longer than s, we can confine ourselves to the limiting probability distribution of for large 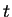$t$, where we have that . When we divide by , call , as before, and abbreviate to , (11.2) reduces in the limit to

Starting with , and using (11.7) in the form

we find by induction that . This relation determines the probabilities up to an arbitrary factor. Obviously, we must have that . The series is well known as the modified Bessel function. So . We therefore arrive at

This probability distribution relates to the Poisson distribution by just squaring the Poisson probabilities and renormalizing to assure that the sum of the probabilities remains 1. The normalizing constant in (11.8) compares with in the Poisson distribution. Since , so , the expected number of protons equals . This is lower than the value , which should be expected on the basis of the deterministic model. This is obvious when we obtain the variance by summing (11.7) for It is found to be . Although it is less than the variance of a Poisson distribution with the same mean it is still considerable for small , as is illustrated in Fig 11.1, which shows that the 95% confidence interval of the pH in a cell of neutral pH ranges from 6.85 to 7.15.

The lifetime of a randomly selected water molecule, a hydroxylion and a hydronium ion follow an exponential distribution with mean , i.e. some h, for water and , i.e. some s, for both ions at C. Diffusion causes these particles to displace in time, 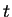$t$, over a mean distance of , where denotes the diffusion coefficient. For HO, OH and H, the latter is 2.26, 5.3 resp. at C. The mean total lifetime displacement in an unbounded body of pure water is thus 1.37cm, 3.26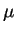$\mu$m and 4.32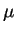$\mu$m, as a crow flies. This means that the limited size of a cell is likely to influence the transport, even apart from influences exercised by, e.g. the membrane. We made some simplifying assumptions. The first one is that the cell consists of pure water, which is obviously not true. Its cytoplasma is well buffered. Although a full analysis would certainly be immensely complex, it is by no means certain that the stochastic fluctuations are more restricted in buffered mixtures. Buffers primarily balance net fluxes, but we did not discuss that situation. The assumption that water molecules dissociate independently from each other is hard to test at the moment. The significance of the weak bonds certainly depends on temperature. The intention of the example is to draw attention to the odd behaviour of the concept proton 'concentration' in small bodies. It might be relevant e.g. when we measure enzyme performance in well mixed extracts and try to evaluate its consequence for the living cell.