

Next: Bibliography
Up: exam
Previous: Key words
The number of described living species still increases
dramatically in groups like bacteria, mites and insects. In
groups like vertebrates or spermatophytes, the number of
described living species shows signs of saturation. How about the
number of extinct species? The conditions allowing fossilization
to occur are rare. Most layers containing fossils are
inaccessible. The number of discovered accessible layers
gradually increases with research intensity. Here we will try to
use preliminary knowledge about the number of living species for
estimating the number of extinct ones.
Suppose that a species gives rise to a new one with a constant
probability rate, say , and that it becomes extinct with
another constant probability rate, say 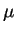 . The latter implies
that the existence time of a species follows an exponential
distribution, with a mean existence time of . If
denotes the number of living species at time
. The latter implies
that the existence time of a species follows an exponential
distribution, with a mean existence time of . If
denotes the number of living species at time 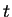 , the
cumulative number of species and the simultaneous
probability that the number of living species equals and that
the cumulative number of species equals , then
can be expressed as a function of
:
, the
cumulative number of species and the simultaneous
probability that the number of living species equals and that
the cumulative number of species equals , then
can be expressed as a function of
:
When we transport the term from the left to the
right, divide both sides by and let
, we arrive at
This simple model defines the probability evolution of both
numbers of species, if we specify the initial condition, e.g.
. So we start with one single species for sure. The
marginal probability evolution of (, obtained by dropping the
index in (12.2),) is known as the linear birth and
death process. We can extract useful information from
(12.2), without actually solving the complete
probability distribution as a function of time.
The expected number of living species, , is found from
(12.2) by multiplying both sides with and summing
over all and . It is for this purpose convenient to define
for negative values of and as well, but put
them equal to zero. This allows us to sum over
We then arrive at
For
, we can solve :
In a similar way, we can multiply both sides of (12.2)
by , sum over all and , arriving at
For
, we can solve :
As an aside, we can evaluate the variance of as follows.
First we multiply both sides of (12.2) by and
sum over all and , arriving at
We then subtract the derivative of , which is
:
For
and noting, in general that
has
as solution, we find
This means that the variation coefficient of is given by
So, as for branching processes, the variation coefficient
approaches a constant value. This is not mere coincidence,
because the linear birth and death process can be conceived as a
branching process by letting the generation time shrink to an
infinitesimally small time increment , while the
offspring distribution for 0,1 or 2 young has been tied to this
increment via the probabilities
,
and
.
In a similar way, we obtain
which gives for
:
and
which gives for
:
from which follows that
) for large 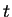 , and that the correlation coefficient
between and approaches 1 for large
, and that the correlation coefficient
between and approaches 1 for large 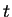 .
The expected number of extinct species is given by
. Using (12.6), we find that
. Since
.
The expected number of extinct species is given by
. Using (12.6), we find that
. Since 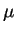 equals
(mean species existence time) and equals (ln
expected no of living species)/(evolution time), we have that
equals
(mean species existence time) and equals (ln
expected no of living species)/(evolution time), we have that
For vertebrates, which fossilize relatively well, due to their
hard bones, the evolution time took some 600 Ma to arrive at some
42000 living species. The mean existence time of vertebrate
species is estimated to be some 2-3 Ma, based on fossil records,
which means that for each living species, we expect some
600/(2.5 ln 42000) 23 extinct ones. The values for
and 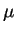 might differ between phyla. If we roughly
estimate 30 million living eukaryotic species to exist, which
took some 2000 Ma to evolve, and if we adopt the vertebrate mean
species existence time, we expect some 46 extinct species for
each living one.
This model is irrealistically simple. This is obvious from the
fact that, for this model, the extinction probability of a richly
diversified group is extremely small. Yet such groups, like
trilobites, ammonites and dinosaurs, became extinct, nonetheless.
At present, the possible occurrence of periodic mass extinctions
is in hot debate. Such complicating phenomena would only increase
the number of extinct species to be expected. The above
calculations could therefore be considered as a lower bound on
the number of extinct species.
During the last 300 year, 150 vertebrate species have been
recorded to became extinct, mainly due to direct or indirect
action of man. The expected extinction rate equals
, which amounts to some 5.6 species in the last 300 year. The
proper answer to the question posed in the title is therefore:
too many!
Further reading on vertebrate evolution: [#!Carr88!#];
On 'natural' and man-induced extinctions: [#!Stan87!#,#!Lewi86!#].
Example 6 for extinction and variation coefficients in branching
processes.
might differ between phyla. If we roughly
estimate 30 million living eukaryotic species to exist, which
took some 2000 Ma to evolve, and if we adopt the vertebrate mean
species existence time, we expect some 46 extinct species for
each living one.
This model is irrealistically simple. This is obvious from the
fact that, for this model, the extinction probability of a richly
diversified group is extremely small. Yet such groups, like
trilobites, ammonites and dinosaurs, became extinct, nonetheless.
At present, the possible occurrence of periodic mass extinctions
is in hot debate. Such complicating phenomena would only increase
the number of extinct species to be expected. The above
calculations could therefore be considered as a lower bound on
the number of extinct species.
During the last 300 year, 150 vertebrate species have been
recorded to became extinct, mainly due to direct or indirect
action of man. The expected extinction rate equals
, which amounts to some 5.6 species in the last 300 year. The
proper answer to the question posed in the title is therefore:
too many!
Further reading on vertebrate evolution: [#!Carr88!#];
On 'natural' and man-induced extinctions: [#!Stan87!#,#!Lewi86!#].
Example 6 for extinction and variation coefficients in branching
processes.


Next: Bibliography
Up: exam
Previous: Key words
Theoretische Biologie
2002-05-01