

Next: Bibliography
Up: exam
Previous: Key words
In a constant environment, a population of bacteria is growing
exponentially after some lag phase, both in number as in biomass,
i.e. the change in biomass is proportional to the biomass itself.
Almost all chemical reactions in the synthesis of biomass are enzyme
mediated. Yet enzymes in isolation do not increase autocatalytically.
This contradictions first calls for a closer analysis.
Suppose that we have two enzymes each of which increases its substance
by the addition of something derived from the working of the other.
Then we shall have
Think e.g. of the interplay of nucleic acids and proteins, each
of which playing a decisive role in the synthesis of the other. In
order to obtain the solution of (13.1), we first write it as
If is the matrix with eigenvectors of in its
columns, and the diagonal matrix with
eigenvalues, so
, the solution of
(13.2) can be written like
The eigenvalues of are easily found to
be
, and
with
. Substitution finally results in
with
and
.
This leads to
Ultimately, the second term in (13.4) vanishes and
the ratio becomes constant at value
and the population grows exponentially. So the cyclic
autosynthetic reactions as modelled in (13.1) is
consistent with exponential growth of biomass, indeed.
For the purpose of, e.g., relating the chemical composition of
cells to that of the medium, one needs cells growing at steady
state (here: growing exponentially). After inoculation, the
culture usually shows a lag phase (i.e. a deviation from
exponential growth, which becomes apparent by plotting the
logarithm of the number of cells against time). So we have to
wait a while before taking the sample material. Now, let us
study the length of the lag phase,
, after a
(momentary) transition from an environment in which the
population was growing exponentially at rate , into and
environment in which the population eventually will grow
exponentially at rate . If both and
are proportional to 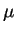 , there will be no lag phase at all,
i.e.
. It seems realistic to assume that only
one, say , is increasing with
, there will be no lag phase at all,
i.e.
. It seems realistic to assume that only
one, say , is increasing with 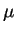 , while the other
remains constant, so
.
From a mathematical point of view, we have to wait infinitely long for
exponential growth, since the second term in (13.4)
vanishes only asymptotically. Being practical, let us accept
exponentiality, if the relative error of the number of cells is less
than a small fraction , i.e.
, where represents the first term in
(13.4), i.e.
, while the other
remains constant, so
.
From a mathematical point of view, we have to wait infinitely long for
exponential growth, since the second term in (13.4)
vanishes only asymptotically. Being practical, let us accept
exponentiality, if the relative error of the number of cells is less
than a small fraction , i.e.
, where represents the first term in
(13.4), i.e.
.
This leads to
The same can be done for , of course, but this will lead again to
relation (13.5). When we choose a certain value for , we
can solve the length of the lag phase 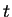 , given
and . The solution is
, given
and . The solution is
The range of values for and is restricted to , because for negative values, the only steady state is that of
being extinct, while values larger than the maximum growth rate
are biologically impossible. A natural scaling for the length
of the lag phase is therefore the dimensionless variable
, expressed in terms of the dimensionless arguments
. We arrive at
A plot of (13.7) is given in Fig.13.1. If and
differ only a little bit, i.e. when
,
the apparent lag phase is zero, which is the result of our acceptance
of a relative error of . This is a bit artificial, which becomes
obvious when we could slowly increase or decrease 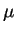 . We would have
to wait a time zero for each incremental change, in other words, we
would not have to wait at all for any change. The relative errors
would built up this way, far beyond our setting of , of course.
Apart for this artifact, some rather counter-intuitive results are
obvious from Fig.13.1. For, the length of the lag phase in an
up shift, is not equal to that of a down shift, i.e.
. Further:
Starting from a small initial growth rate, we have to wait longer to
reach steady states for a bit higher new growth rate, than for a much
higher one. Finally: We have to wait really long in case of a
significant down shift. This illustrates that it is extremely
difficult to standardize the cells to conditions of a small growth
rate. This is important, because this is the usual condition outdoors,
which we need to reach when we want, e.g, to exclude growth for the
study of maintenance.
These results are possibly easier to remember, when we express the lag
phase in the number of division intervals in the new situation, where
. In steady state we have
for the number of bacteria at time , which equals , for time
. If we divide the lag
time in (13.6) by this division interval, we arrive at
. We would have
to wait a time zero for each incremental change, in other words, we
would not have to wait at all for any change. The relative errors
would built up this way, far beyond our setting of , of course.
Apart for this artifact, some rather counter-intuitive results are
obvious from Fig.13.1. For, the length of the lag phase in an
up shift, is not equal to that of a down shift, i.e.
. Further:
Starting from a small initial growth rate, we have to wait longer to
reach steady states for a bit higher new growth rate, than for a much
higher one. Finally: We have to wait really long in case of a
significant down shift. This illustrates that it is extremely
difficult to standardize the cells to conditions of a small growth
rate. This is important, because this is the usual condition outdoors,
which we need to reach when we want, e.g, to exclude growth for the
study of maintenance.
These results are possibly easier to remember, when we express the lag
phase in the number of division intervals in the new situation, where
. In steady state we have
for the number of bacteria at time , which equals , for time
. If we divide the lag
time in (13.6) by this division interval, we arrive at
The role of and in (13.8) is now symmetric,
and the largest number of division intervals in the lag phase,
i.e. when or equals 0, is
.
See Fig.13.1.
The model (13.1) can easily be extended to more than two
types of enzyme, in which case the population growth rate, 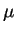 ,
equals the geometric mean of the rate of increase of the different
enzyme types,
. It remains rather
easy, because of the linearity. Such a system can be conceived as a
first approximation to the more usual hyperbolic rate functions, where
the substrate concentrations are small with respect to the saturation
constants (see example 10).
Although the presented modelling of population growth in
terms of chemical reactions is considered standard in
microbiology (, the classical results given in Hinshelwood (1952)
are followed here), a warning seems appropriate for skipping
levels of organisation (here: the cell), and a too loose
reference to variables that can be measured directly or
indirectly.
Further reading for a classical and still relevant work on
enzyme performance in growing cells: [#!Hins52!#].
,
equals the geometric mean of the rate of increase of the different
enzyme types,
. It remains rather
easy, because of the linearity. Such a system can be conceived as a
first approximation to the more usual hyperbolic rate functions, where
the substrate concentrations are small with respect to the saturation
constants (see example 10).
Although the presented modelling of population growth in
terms of chemical reactions is considered standard in
microbiology (, the classical results given in Hinshelwood (1952)
are followed here), a warning seems appropriate for skipping
levels of organisation (here: the cell), and a too loose
reference to variables that can be measured directly or
indirectly.
Further reading for a classical and still relevant work on
enzyme performance in growing cells: [#!Hins52!#].
Figure:
Contours for the length of the lag phase following a transition from
one exponential growth rate to another, accepting a relative error
of 0.05. The growth rates are expressed as fractions of the maximal
growth rate. The contours of values 5, 2.5, 1, 0.5 and 0 are shown
for the time lag times the maximum growth rate times .
|


Next: Bibliography
Up: exam
Previous: Key words
Theoretische Biologie
2002-05-01