

Next: Shape constraints for isomorphs
Up: exam
Previous: Key words
From a cell physiological point of view, the mechanism of the
opening and closing of ion channels in nerve cells is very
important. However, it is not so easy to perform experiments
at molecular level, so these mechanisms must be inferred
indirectly from measurements of total cell performance. It is
possible to measure the electrical flux between two clamps
attached to a dendrite of a single cell. It varies somewhat in
time, and the first question is: can we make use of these
variations in time to disentangle the opening and closing of
individual channels? With aid of a model for the behaviour of
these channels, it is possible indeed.
The argument runs as follows. Assume that the electrical
flux is proportional to the number of ion channels that are
open. Assume further that the probability that a randomly
chosen closed channel will open in an incremental time
interval equals
. Similarly, the
probability that a randomly chosen open channel will close in
that interval is assumed to be . For the moment
we will assume that the probability rates and  are constant and that the probability that a channel opens as
well as closes in is negigibly small. When
denotes the number of channels between the clamps, the
number of channels that are open and
are constant and that the probability that a channel opens as
well as closes in is negigibly small. When
denotes the number of channels between the clamps, the
number of channels that are open and 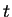 the time, the
probability that there are open channels at time
the time, the
probability that there are open channels at time 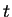 is
given by
is
given by
To simplify the notation, we assume that
.
If we let approach to zero, we arrive at
This equation describes the opening and closing behaviour of ion
channels, in which we consider , and 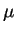 as parameters
to be estimated from a continuous registration of the electrical flux,
so the number of open channels. With a very small probability, all
channels are open at a given time, so when we wait long enough, the
maximum flux over a very long time bears information about the number
of channels . However, it is very hard to keep conditions constant
over such long a period. Therefore we will not make use of this
possibility. What we will do is use the mean, the variance and the
autocovariance function to lead us to the three parameters. The mean
and variance can be deduced from the equilibrium distribution for ,
i.e. the case where
. Using (16.2)
we obtain
as parameters
to be estimated from a continuous registration of the electrical flux,
so the number of open channels. With a very small probability, all
channels are open at a given time, so when we wait long enough, the
maximum flux over a very long time bears information about the number
of channels . However, it is very hard to keep conditions constant
over such long a period. Therefore we will not make use of this
possibility. What we will do is use the mean, the variance and the
autocovariance function to lead us to the three parameters. The mean
and variance can be deduced from the equilibrium distribution for ,
i.e. the case where
. Using (16.2)
we obtain
This we recognize as the binomial distribution with mean
and variance
.
The straightforward way to obtain the covariance function is first to
solve from (16.2) from the initial condition
. Let us call this solution . When we denote
the equilibrium distribution by , the (equilibrium)
autocovariance function is given by
. The problem now is that it is very laborious to
obtain . In this case it is helpful to note that we do
not need it explicitely, we only need it as a weighted sum over all
and . We therefore try to convert the set of differential
equations of all the 's into one for the autocovariance
function. We note that
, with . From (16.2),
we obtain
After some manipulation, we obtain the simple expression
which leads to
. So the
autocovariance function decreases exponentially with rate
.
It is instructive to relate this model formulation with a very simple
deterministic one, where we assume that is large enough to allow a
continuous approximation. When the opening of channels is proportional
to the number of closed channels and the closing of channels is
proportional to the number of open channels, we have
. The
solution is
, and we
recognize
as the relaxation time.
Back to the stochastic model now. The simplest way to proceed
is to uncover from . We can do this
e.g. by plotting against time and fit a straight line.
Although this procedure must be classified as "quick and
dirty", it is not at all obvious how to formulate a "clean"
procedure. Next we multiply by and obtain
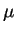 . Subsequently we uncover and .
The ability to disentangle the opening from the closing rate can be
very valuable in the experimental research to which (environmental)
factors influence both mechanisms. The constraint that and
. Subsequently we uncover and .
The ability to disentangle the opening from the closing rate can be
very valuable in the experimental research to which (environmental)
factors influence both mechanisms. The constraint that and
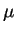 are constant can be relaxed to the constraint that the rate at
which they vary is small with respect to .
are constant can be relaxed to the constraint that the rate at
which they vary is small with respect to .
Filename: ex016; Date: 1990/09/02; Author: Bas Kooijman


Next: Shape constraints for isomorphs
Up: exam
Previous: Key words
Theoretische Biologie
2002-05-01