

Next: Bibliography
Up: exam
Previous: Key words
The Ames test is a bioassay for testing the mutagenic potential of
chemicals on the basis of the frequency of backward mutations in
histidine auxotrophic mutants of the pathogenic bacterium
Salmonella typhimurium (i.e. these bacteria have been mutated
such that they are no longer able to synthesize the amino acid
histidine themselves, so they need it in the medium). At the start of
the experiment, a certain amount of (primairy) histidine auxotrophs
are inoculated on an agar plate containing a rich medium with,
however, a little bit of histidine and the chemical to be tested.
(Usually, there are several plates with different concentrations of
chemical.) The incolated bacteria grow and divide, until the histidine
is exhausted. So each produces a micro-colony, usually consisting of
some 100 bacteria. If one or several bacteria have been permanently
converted to the prototrophic state, however, its colony will continue
to grow and will become visible with the naked eye. Its is then called
a revertant colony. The growing state seems to be a condition for the
expression of the backward mutation. So, no visible mutations occur
after colony growth ceased due to histidine limitation. For mutagenic
chemicals, the number of revertant colonies generally increases
linearly with its concentration, at a rate that is taken to be
proportional to its mutagenic potential. Let us study the quatitative
aspect.
To derive an expression for the number of revertant
colonies, we first need the fixation probability , which
is the probability that a prototrophic cell of age a at time
zero will grow into a revertant colony after the moment the
histidine is exhausted. Generally, this fixation probability
is less than 1 because prototrophic cells may become extinct
due to conversion to multiple auxotrophy. This extinction
probability is easily found from the probability generating
function, , of the number of prototrophic cells arising
from a prototrophic cell after division, i.e.
, where
and
is the conversion probability from a prototrophic cell into a
multiple auxotrophic one in a period 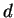 , i.e. the division
interval. The extinction probability
, of prototrophic cells starting with a prototrophic
one of age
, i.e. the division
interval. The extinction probability
, of prototrophic cells starting with a prototrophic
one of age 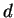 is given by
. If the probability rate for
conversion of a multiple auxotrophy to a primairy auxotrophy
or prototrophy is neglibibly small, and if the conversion
probability rates from primary auxotrophy and prototrophy to
multiple auxotrophy is equal and constant at value ,
say, we have
. This leads to
. For an arbitrary initial age
, we should account for the probability of conversion to
multiple auxotrophy before the moment of first division, so
is given by
. If the probability rate for
conversion of a multiple auxotrophy to a primairy auxotrophy
or prototrophy is neglibibly small, and if the conversion
probability rates from primary auxotrophy and prototrophy to
multiple auxotrophy is equal and constant at value ,
say, we have
. This leads to
. For an arbitrary initial age
, we should account for the probability of conversion to
multiple auxotrophy before the moment of first division, so
where the + sign indicates the maximum of zero and the term
within the brackets.
Suppose that we inoculate with cells (usually some )
and that the amount of histidine is just enough for the
formation of cells on the plate. Suppose further that the
division interval 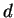 is constant. The number of cells on
the plate then grows exponentially in time, i.e.
, as long as the histidine is not limiting. This
occurs at time
is constant. The number of cells on
the plate then grows exponentially in time, i.e.
, as long as the histidine is not limiting. This
occurs at time 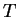 , found from , giving
. In writing an expression for the
probability on a revertant colony, we have to realize that the
inoculated cells as well as the cells present at
, found from , giving
. In writing an expression for the
probability on a revertant colony, we have to realize that the
inoculated cells as well as the cells present at 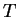 , have not
been exposed to the chemical during their full life cycle. To
deal with this fact, we partition
, have not
been exposed to the chemical during their full life cycle. To
deal with this fact, we partition 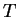 as
, where
and . Suppose that each
inoculated cell has a probability of being primary
auxotrophic and of being prototrophic. If the
probability rate of conversion from primary auxotrophy to
prototrophy is small and constant at value
as
, where
and . Suppose that each
inoculated cell has a probability of being primary
auxotrophic and of being prototrophic. If the
probability rate of conversion from primary auxotrophy to
prototrophy is small and constant at value 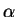 , say, the
probability, , that an inoculated cell of age
will grow into a revertant colony is given by
, say, the
probability, , that an inoculated cell of age
will grow into a revertant colony is given by
Suppose that we start with the stable age distribution for the
inoculated cells, i.e.
.
The probability that a randomly chosen cell will then grow into a
revertant colony is after some calculations found to be
which reduces for negligibly small to
The number of revertant colonies will be binomially
distributed, but in view of the small number of revertant
colonies with respect to the number of inoculated cells, it is
safe to use the approximation with the Poisson distribution
with parameter . If each molecule of the chemical has
an equal (and small) probability of causing a mutation, a will
be proportional to the concentration. One can use likelihood
based linear Poisson regression, to obtain the propartionality
constant from the number of revertant colonies at several
concentrations of test compound.
In conclusion, (5.3) confirms the empirical
observation that the mean number of revertant colonies depends
linearly on the concentration of chemical. However, it also
reveals that a number of other factors contribute as well,
like the age distribution and the amount of inoculated cells,
the amount of histidine supplied and the division interval
(and so the composition of the medium). In practice these
problems are "solved" by standardization. Additional
complications arise if the chemical also affects growth (so
prolonging the period of exposure), particularly if the agar
contains slightly mutagenic compounds (due to autoclavation,
and referred to as "background" mutations).


Next: Bibliography
Up: exam
Previous: Key words
Theoretische Biologie
2002-05-01