

Next: Bibliography
Up: exam
Previous: Key words
Suppose that in a constant environment, the survival
probability of a female individual with age , is given by
, and that its reproduction rate is . Let
denote the number of females at time 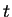 having
an age somewhere in the interval
. Then the
total number of individuals, , is given by
. How will the population develop
if we specify the composition of a population at time
having
an age somewhere in the interval
. Then the
total number of individuals, , is given by
. How will the population develop
if we specify the composition of a population at time 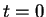 ,
say by
? To evaluate the population, we need
to know the birth rate at time
,
say by
? To evaluate the population, we need
to know the birth rate at time 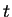 , . If the reproduction
rate was a constant , we could easily state .
However, because reproduction rate is age dependent, we must
calculate birth rates in every 'age class' and 'add them up', or in
mathematical terms
, . If the reproduction
rate was a constant , we could easily state .
However, because reproduction rate is age dependent, we must
calculate birth rates in every 'age class' and 'add them up', or in
mathematical terms
So if we know we can calculate . On the
other hand we can see that is determined by in
the following way: individuals having age at time 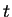 are the
individuals which were born at time and have survived up to
age . Again in mathematical terms
are the
individuals which were born at time and have survived up to
age . Again in mathematical terms
Notice that the right-hand side of this expression
contains in fact a probabilistic term, . On the population
level it can be interpreted as 'the fraction surviving age '.
Substitution of (4.2) in (4.1) gives the following
integral equation for
In this equation our assumed knowledge of the population at time 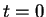 has not yet been used. This can be achieved by making a census in
time in (4.3). If we can rewrite (4.2) as
Substitution in (4.3)
results in
has not yet been used. This can be achieved by making a census in
time in (4.3). If we can rewrite (4.2) as
Substitution in (4.3)
results in
This equation is known as the renewal equation. It can be read as
follows: births at time 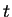 originate from individuals born since
originate from individuals born since
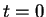 and from individuals already present in the population at
and from individuals already present in the population at
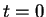 . The latter term is usually called .
We assume there is some value such that and
for ( can be interpreted as the maximal
age). Then for . Now suppose that the solution of
(4.4) is of the form
, for some value
for , then (4.4) reduces (for ) to
. The latter term is usually called .
We assume there is some value such that and
for ( can be interpreted as the maximal
age). Then for . Now suppose that the solution of
(4.4) is of the form
, for some value
for , then (4.4) reduces (for ) to
Dividing by we get the following
equation for
This equation is known as the characteristic equation.
It is possible to show that, under some smoothness restrictions on
the reproduction function , this equation has exactly one
real root . The other roots are complex
and have a real part smaller than . The general solution
appears to be a linear combination
. For
large values of 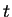 the exponential will be
dominant, so the the asymptotic solution will be
. (The smoothness restrictions on are
violated if for instance reproduction is only possible at certain
particular ages. The information about the composition of the
initial population then never gets lost.)
From (4.2) it follows that
and that
. This implies that represents the (eventual)
population growth rate and that not only the total number of
individuals is eventually growing exponentially, but also the number
in each age class. Now we define the so-called stable age distribution
as
the exponential will be
dominant, so the the asymptotic solution will be
. (The smoothness restrictions on are
violated if for instance reproduction is only possible at certain
particular ages. The information about the composition of the
initial population then never gets lost.)
From (4.2) it follows that
and that
. This implies that represents the (eventual)
population growth rate and that not only the total number of
individuals is eventually growing exponentially, but also the number
in each age class. Now we define the so-called stable age distribution
as
It can be conceived as the probability
density of the age of a randomly selected individual in a
really large population, exponentially growing in a constant
environment.
As an example, consider a micro-organism growing exponentially from
volume to volume in interval , after which it
divides into two parts of volume again. Here
for
. If there are no actual deaths, we
can fictively put
and
. From (4.5) we obtain
. In
principle, a population of such micro-organisms has no stable age
distribution because of the mentioned phenomenon that the initial age
distribution continues to exercise its influence. In practice however,
there will be enough scatter among the division intervals of the
daughter cells to destroy synchronicity. It seems safe therefore to
neglect this problem and obtain from (4.6) the semi-stable
age distribution
Alternatively, we can recast this into the semi-stable size
distribution by substituting
and
into (4.7). We obtain
. See Fig.4.1. Thus we
see that the size distribution is independent from the population
growth rate. In practice it will be dependent nonetheless, because at
high population growth rates cells start a new DNA duplication cycle,
before the former one is fully completed. This results in increasing
cell sizes at high population growth rates.
The notion of stable age distributions is important in the
theory of population dynamics. For practical purposes it is
essential to realize that they eventually occur only in
populations living in constant environments. This condition
will not occur for a long period, outdoors. Apart from
seasonal changes in the environment, an exponentially growing
population will soon exhaust its resources, depending on the
population growth rate.
Figure 4.1:
The stable age (left) and size (right) distribution of exponentially
growing micro-organisms that divide in two parts.
|


Next: Bibliography
Up: exam
Previous: Key words
Theoretische Biologie
2002-05-01